Prologue to Equideductive TopologyPaul Taylor |
Equideductive topology is a new programme that seeks an inherently computable re-axiomatisation of general topology, in order to extend the one provided by Abstract Stone Duality beyond the class of locally compact spaces. As in ASD, every term will automatically denote both a continuous function and a program that is in principle executable. The new system of types, on the other hand, will allow objects to be formed using a “comprehension” notation, {x:X ∣ p(x)}, like that in set theory, in which p(x) belongs to a quite rich predicate calculus. The nature of the generalisation from ASD is not simply a matter of relaxing the old definitions, as one might imagine from point–set topology, but of passing from direct computation to proof.
ASD began from an idea in pure category theory and was developed as far as some simple applications in real analysis. It provides a logic of open subspaces, classified by the Sierpiński space Σ, in particular with universal quantification ∀K:ΣK→Σ over any compact space K.
This “internal” logical structure within the object Σ matches an “external” logic of subobjects, where by a subobject we mean a certain kind of map between two objects in the wider category. Underlying this, a kind of “type theory” is needed that actually constructs the subobjects which are classified by terms of type Σ, as well as more ordinary connectives such as products and exponentials. In ASD, this type theory was obtained from the original categorical idea, namely that the adjunction Σ(−)⊣Σ(−) be monadic.
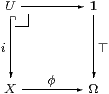
This way of organising the logic of open subspaces in topology was inspired by the corresponding situation in set theory that is captured in the notion of an elementary topos. Recall that the object Ω in a topos classifies subobjects

in the sense that any mono i:U↪ X is the inverse image (pullback) of the map ⊤:1→Ω along a unique map φ:X→Ω.
This correspondence between subobjects of X and maps X→Ω extends to one between categorical operations on subobjects and the internal logical structure of Ω. For example, the external intersection of two subobjects is given by a pullback in the category, whilst the corresponding internal conjunction is a binary lattice operation ∧:Ω×Ω→Ω, as the diagrams in Geometric and Higher Order Logic illustrate. Using finite limits and exponentials, the whole of intuitionistic higher-order predicate calculus may be interpreted in the external and internal logic of the topos.
The application of similar ideas to topology and recursion theory on which ASD relied was pioneered by Giuseppe Rosolini. In topology, the Sierpiński space Σ takes the place of Ω and, instead of arbitrary subspaces U↪ X in the pullback square above, we just have open ones. Rosolini actually introduced these ideas in order to describe a similar object in recursion theory that classifies recursively enumerable subsets.
Whereas there is only one kind of subobject in set theory, in topology we need to consider many other kinds besides open ones, such as closed, compact, overt and dense subspaces. In fact, the other point of the Sierpiński space classifies closed subspaces, but there is no classifier for other kinds of subspace. Instead there are other ad hoc notations, such as {x:X ∣ λφ.φ x⊑ A}, which was used in A Lambda Calculus for Real Analysis for the compact (saturated) subspace whose Scott-open filter of open neighbourhoods is classified by A:ΣΣX. However, such a subspace need not in general be definable from the ASD type theory that arises from the monadic adjunction Σ(−)⊣Σ(−). Semantically, this is because a compact subspace of a (non-Hausdorff) locally compact space need not itself be locally compact, although we can give a meaning to this notation amongst sober topological spaces.
Whilst this ad hoc notation diverges to some extent from the principles of ASD, this is the idea that we shall develop into equideductive topology. It will turn out that we can legitimately see any (in)equality such as λφ.φ x⊑λφ.Aφ between λ-terms as a “universally quantified” predicate
| ∀φ.(φ x=⊤)⇒(Aφ=⊤), |
whilst it is well known that the inequality ⊑ in any lattice can be rewritten as an equation. Then the equations on either side of ⇒ can themselves be generalised to quantified predicates.
However, the universal quantifier ∀ here is not the same as the ∀ that was used for a compact space (hence the change of symbol). If ∀ ranges over a lattice such as ΣX and we apply it to a formula Fφ of type Σ, by monotonicity of F it just trivialises to
| (∀φ:ΣX.Fφ) ⇔ F⊥. |
In any case, this is irrelevant because the body φ x⇒ Aφ of the quantified formula that we are considering is not a term of type Σ anyway. The new, non-compact, quantifier ∀ is the one that we have already mentioned in the form of an infinite intersection and will be the principal symbol of equideductive logic. This will provide a type-theoretic framework in which to discuss various kinds of subobjects in a syntactic fashion.
In fact we shall see in Equideductive Topology that a space K is compact iff the equideductive quantifier ∀K is represented by a term A in the sense that
| ∀ x:K. (φ x=⊤) ⊣⊢ (Aφ = ⊤), |
and then we write ∀ x.φ x for Aφ:Σ. (In the concrete syntax, ∀ binds more tightly than =, whereas ∀ binds less tightly.) We could say that, in this case, ∀K takes the open subspace φ to another open subspace Aφ, instead of to a general one. No such distinction is needed in set theory because all subobjects are open.
Evidently the new symbols ∀ and ⇒ are a kind of syntax. When the category is a topos, these are algebraic structure on Ω, and we shall show in Equideductive Topology that the situation characterises toposes. In topology, on the other hand, they take us outside the term calculus of Σ.
Categorically, we are giving names to increasingly general kinds of subobject that are built up from equalisers using partial products. These names are formed from those of the many morphisms in the diagrams .
Syntactically, we can therefore think of the new calculus as generated in the following way. Open subspaces are primitive and the logic of Σ allows us to apply certain logical operations to them. However, if we break the rule for ∀ that it can only range over a compact space, or use entirely illegitimate symbols such as ⇒ and ¬, then we go outside the world of open subspaces into a more general one. Nevertheless, this logic can still be given a meaning by understanding it to apply to the points of the space, yielding a subset; this can be treated as a subspace if we re-impose the induced topology.
Equideductive topology will interpret this predicate calculus without abandoning the topological structure along the way. In this first paper we shall develop the basic form of the logic as a formulation of the external logic of subobjects, without assuming any internal structure on the object Σ. The predicates are names for (recipes for constructing) subobjects based on the morphisms that are involved. The simplest such subobjects are given by equalisers, and more complicated ones by the generalised equalisers that we call partial products in Equideductive Categories and their Logic. In Equideductive Topology we put a lattice structure on Σ and require its order to agree with ⇒: it is this that relates ∀ and ∀ as above and, as in ASD, makes the theory begin to look like topology.
The same ideas transfer from general topology to computability, following the analogy that Dana Scott exploited so successfully. In particular, all computable functions are continuous. ASD has shown that topology can be redefined to secure the converse, so for example the recursively enumerable subsets of ℕ provide its topology.
Other kinds of subspaces will be defined in equideductive topology using the predicate calculus that we have sketched. This accords with another powerful analogy in foundational studies, namely that between computation and proof. Whereas open subspaces are computationally observable properties, general subspaces are provable ones.
In summary, taking account of all of these ideas, the new logic will have two levels:
| lower level open subspaces | general subspaces upper level |
| locally compact spaces | “general” spaces |
| observable properties | provable properties |
| computation | proof |
| terms σ,φ,… of type Σ | predicates p(x) |
| (in)equalities (⊑) between terms | (bi)implications (⇒) between predicates |
| sober λ-calculus | equideductive logic |
| ⊤, ⊥, ∧, ∨, ∀, ∃ | ⊤, ⊥, &, ⋎, ∀, Э |
The development of this new system will require a number of papers. The ASD research programme was intended to develop its structure in several layers:
It is necessary to repeat this task because the inadequacy of the old programme lay in the choice of structure at its bottom level (a). Also, the plan was itself emerging in them, the earlier papers did not express it as clearly as one might like. We would hope to follow it more closely the second time around, filling in details that were inadequately documented before.
The following papers are therefore envisaged:
In order to try to develop the whole programme in a coherent way, I intend to set out drafts of all of these papers before finalising the mathematical details in any of them or submitting them to a journal.
We have already hinted that the equideductive programme represents a retreat from the original categorical principles of ASD. These emphasised monadicity of the adjunction Σ(−)⊣Σ(−) that holds for Σ≡Ω in a topos and sought some more powerful exactness property that would be suitable for general topology beyond local compactness.
I believed that some categorical manipulation of either the category of locales or Scott’s category of equilogical spaces would yield a new model with the properties that I envisaged. However, this was quite mistaken and lost a great deal of time.
In the process, it became apparent to me that, in any category of the kind that I wanted, there would be a certain simplification of equalisers and exponentials, whilst the definition of equilogical spaces also enjoys this simplification. A construction similar to Scott’s was therefore “the only game in town”. The heavy dependence of equilogical spaces on their underlying sets could be eliminated by using what has evolved into equideductive logic. An equideductive category is therefore intended to be one that lies within its cartesian closed extensions in a simple way and has such an extension that is not much more complicated.
A useful metaphor is that ℝ lies within its algebraic closure ℂ in a simple way. Since Gauss proved the so-called fundamental theorem of algebra in 1797, we have known that ℂ consists in a sense of just two copies of ℝ. Back in the sixteenth century, things could have turned out otherwise: perhaps the addition of √−1 might have been the thin end of a wedge that would go on to require roots of ever more complicated polynomials.
Equalisers and exponentials play the roles of subtraction and square roots in this analogy. Like roots of equations whose coefficients are ever more complicated numbers, the combination of these operations quickly become unwieldy: The exponential ΣY of an non-locally compact space Y does not lie within the usual category of topological spaces, which is why we need extensions such as equilogical spaces. However, an equaliser E↣ X⇉ΣY taken in the larger category (but with X in the smaller one) might perhaps fall back into the smaller one. In fact, this happens for sober topological spaces but not for locales.
Because of this injection of ideas from Scott’s equilogical spaces, the greater part of the technology that we shall develop in the new equideductive programme will be consistent with work by other authors that uses equilogical and QCB spaces.
On the other hand, we also need to resolve the mis-match with the objectives of ASD.
Although they were not intended to be so, the ASD papers as they have been published may be read as an account of locally compact spaces. The equideductive programme will be developed in a way that is consistent with this reading.
However, I envisage further work of a proof-theoretic nature with the goal of identifying a new axiom of “Scott continuity of proofs” that would be a conservative extension of the syntax of equideductive logic but not valid in the traditional semantic models. I hope that this will then provide a model of the categorical principles that I was seeking.
This document was translated from LATEX by HEVEA.