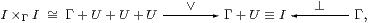



Remark 5.1
Consider the lattice dual of the Euclidean principle,
| σ ∨ F(σ) ⇔ σ ∨ F(⊥), |
where we suppress the parameter x∈ X to σ∈ΣX and F∈ΣX×Σ. Taking F to be ¬¬ in Set or Pos, this yields excluded middle (¬¬σ⇔ σ). Observe that the Euclidean principle and its dual are trivial for σ≡ ⊤ and σ≡ ⊥, and therefore for the classical case Σ≡ {⊥,⊤}. ▫
In topology and recursion, C-morphisms of the form F:ΣY→ΣX preserve directed joins with respect to the semilattice order: they are said to be Scott-continuous (cf. Examples 2.11).
This completely changes the constructive status of the dual Euclidean principle.
The results about open subsets and maps and overt objects that we present later in the paper then have closed, proper or compact mirror images. Note that Scott-continuity of ¬¬ would imply excluded middle.
More basically, any F:ΣY→ΣX is monotone (Remark 3.5) in Pos as well as in topology and recursion, but not in Set. Even though we intend to consider (locally compact) topological spaces X in general, we need only use lattice or domain theory to study ΣX, since this is just the lattice of open subsets of X, equipped with a topology that is entirely determined by the (inclusion) order.
Lemma 5.2
For any exponentiating semilattice Σ,
the functor Σ(−) is order-enriched
iff all functions ΣY→ΣX are monotone,
but then it is contravariant with respect to the order:
if F⊑ G then ΣG⊑ΣF,
and if L⊣ R then ΣR⊣ΣL. ▫
Remark 5.3 In recursion theory,
ΣX consists of the recursively enumerable subsets of X.
By the Rice–Shapiro theorem [Ric56, Ros86]
,
recursive functions F:ΣY→ΣX again preserve directed unions.
The following result has an easier proof in this situation,
where σ∈Σ measures whether a program ever terminates:
then σ⇔ ⋁nσn,
where σn decides whether has finished within n steps
or is still running.
Proposition 5.4
Suppose that C has stable disjoint coproducts
and a dominance Σ that is a distributive lattice.
Then for every element σ∈Σ,
there is some directed diagram d:I→{⊥,⊤}⊂Σ,
only taking values ⊥ and ⊤,
and with I an overt object (Section 7),
of which σ is the join.
Proof Intuitively, σ is ⊤ just on the part U≡ [σ] of the world that it classifies, so σ is the smallest global element that is above the partial element ⊤:U→Σ. Since U is classified, it is open. Also, as it is a subsingleton, it satisfies the binary part of the directedness property. We achieve the full property by using d≡ [⊥,⊤]:I≡ 1+U→Σ.
In more orthodox3 categorical terms, σ:Γ→Σ is a generalised element and classifies i:U↪Γ; then we put I≡ Γ+U and d≡ [⊥,⊤]. Stable disjoint sums in C (Section 9) are needed to show that d:I→Σ is directed and I→Γ is an open map (Section 7). In fact there a semilattice structure
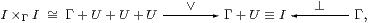
where U×ΓU≅ U since U↪Γ. An element τ∈Σ is an upper bound for the diagram d:I→Σ iff its restriction to U is ⊤, as is the case for σ.
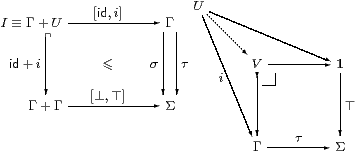
If τ classifies V↪Γ and is a bound then there is a commutative kite, so U⊂ V using the pullback. However, to deduce φ⊑ψ, we need uniqueness of the characteristic maps to Σ, or equivalently the Euclidean principle. ▫
The synthetic form of this argument uses the left adjoint ∃d:ΣΓ×ΣU≅ΣΓ+U→ΣΓ of Σd, for which ∃d(⊥,⊤)≡ φ. Corollary 8.4 discusses I-indexed joins.
[More simply, if we formulate the Scott principle, cf. [E], as
| ξ:ΣN, F:ΣΣN ⊢ Fξ ⇔ ∃ℓ:K N.F(λ n.n∈ℓ) ∧ ∀ n∈ℓ.ξ n |
then the Phoa principle is the special case N≡1.]
Corollary 5.5
The dual of the Euclidean principle is therefore also valid in LKLoc.
By Theorem 3.10,
this says that ⊥∈Σ classifies closed subsets.
Proof By Scott continuity and Remark 5.1 for {⊥,⊤}. ▫
Classically, this is trivial, but we are making a substantive claim here about how the Sierpiński space ought to be defined intuitionistically. This claim is amply justified by the open–closed symmetry that we shall see in this paper and [D]. Indeed Japie Vermeulen has identified the dual Frobenius law for proper maps of locales [Ver94], although he used the opposite of the usual order on a frame, so that φ⊑ ψ would correspond to inclusion of the closed subsets that they classify. André Joyal and Myles Tierney defined the Sierpiński space by means of the free frame on one generator [JT84, §IV 3], and gave a construction in terms of the poset {⊥⊑⊤} that amounts to saying that ΣΣ≅Σ⊑.
[There is a much simpler proof of the dual Euclidean and Phoa principles for locales in §O 7.5.]
Corollary 5.6
By the lattice dual of the results of Section 3,
there is a right adjoint Σi⊣ ∀i
of the inverse image map for
the inclusion of a closed subset
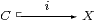
in LKLoc. This satisfies the dual of the Frobenius law,
| ∀i(θ)∨ ψ = ∀i(θ∨ Σiψ) |
for any θ∈ ΣC and ψ∈ΣX, together with Beck–Chevalley again. ▫
The same principle is also valid in (parallel) recursion theory, where Martin Hyland stressed [Hyl91, Assumption 4] that ⊥ should classify co-RE subsets, as well as ⊤ classifying RE subsets. He also stated the following idea as his Assumption 6, although it was only after writing that paper that he attached his former student’s name to it.
Proposition 5.7
Let Σ be an exponentiating object with global elements ⊥⊑⊤
in an internal preorder.
Then the conjunction of
for all F:X×Σ→Σ and σ∈Σ, is the Phoa principle that
any such F is monotone in this sense, and conversely
for each pair of maps φ,ψ:X⇉Σ with φ⊑ψ pointwise,
there is a unique map F:X×Σ→Σ with F(x,⊥)≡ φ(x) and F(x,⊤)≡ ψ(x).
In this case, F is obtained from φ and ψ by “linear interpolation”: Fσ≡ F⊥∨(σ∧ F⊤).
Another way of stating the Phoa principle is that <ev⊥,ev⊤>:ΣΣ→Σ×Σ is mono and is the order relation on Σ, indeed that for which ∧ is the meet and ∨ the join.
Proof [⇒] F must be given by this formula (and so ΣΣ→Σ×Σ is mono) because
| Fσ ⇔ (Fσ∨σ)∧ Fσ ⇔ (F⊥∨σ)∧ Fσ ⇔ (F⊥∧ Fσ)∨(σ∧ Fσ) ⇔ F⊥∨(σ∧ F⊤). |
[⇐] Any function F given by this formula is monotone in σ. With X≡ Σ, we obtain F≡ ∧ from φ≡ λ x.⊥ and ψ≡ id, and F≡ ∨ from φ≡ id and ψ≡ λ x.⊤. Now consider the laws for a distributive lattice in increasing order of the number k of variables involved. For k≡ 0 we have the familiar truth tables. Each equation of arity k≥1 is provable from the ones before when the kth variable is set to ⊥ or ⊤, so let φ⊑ψ:X≡ Σk−1→Σ be the common values; then the two sides of the equation both restrict to φ and ψ, so they are equal for general values of the kth variable by uniqueness of F:Σk→Σ. Finally, σ∧ Fσ⇔ σ∧(F⊥∨(σ∧ F⊤)) ⇔ (σ∧ F⊥)∨(σ∧ σ∧ F⊤)⇔ σ∧(F⊥∨ F⊤)⇔ σ∧ F⊤, and similarly for the dual. ▫
Remark 5.8 Theorem 4.2 and Remarks 4.3(a,c,e,f)
can easily be adapted to show that the Phoa principle holds
in the free model in which Σ is a distributive lattice,
either as the lattice dual result
together with a separate proof of monotonicity, or by expanding polynomials.
For the latter method,
the case of application (4.2(e)) is again the most complicated,
the induction hypothesis being
F⊥⇒ Fσ⇔(F⊥∨σ∧ F⊤)⇒ F⊤.
[This suffers from the same error as Theorem 4.2.] ▫
Definition 5.9
When all maps F:Γ×Σ→Σ preserve the semilattice order
there are two ways of extending this order
to binary relations on any other object X of the category
(not just the retracts of powers of Σ as in Remark 3.5).
They both agree with the concrete order in Cont and
(assuming excluded middle) Pos.
| x⊑Σy if ∀φ∈ΣX.φ x⇒ φ y, |
| x⊑L y if ∃ℓ:Σ→ X.ℓ(⊥)=x ∧ ℓ(⊤)=y, |
Wesley Phoa formulated his principle and introduced the link order to show that the order relation on a limit in his category of domains is given in the expected way [Pho90a, §2.3]. For this to work, ℓ must be unique.
Important though they are in domain theory, these order relations will only be mentioned in this paper in the trivial situation of the following section.


