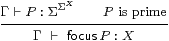 focusI
focusI



In this section we show that SC interprets the restricted λ-calculus, together with the new operation focus. For reference, we first repeat the equation in Remark 4.11.
Definition 8.1 Γ⊢ P:ΣΣX is
prime if Γ, F:Σ3 X ⊢
F P ⇔ P(λ x.F(λφ.φ x)).
Definition 8.2 The sober λ-calculus
is the restricted λ-calculus (Definition 2.1)
together with the additional rules
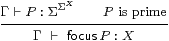 focusI
focusI
|
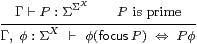 focusβ
focusβ
|
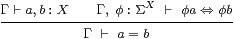 T0
T0
|
The definition thunka = ηX(a) = λ φ.φ a serves as the elimination rule for focus. Using this, equivalent ways of writing the focusβ and η (T0) rules are
| thunk (focusP)=P and focus (thunkx) = x, |
where P is prime.
Remark 8.3 The restriction of focus to primes
is the crucial difference from Thielecke’s force calculus,
and is the reason why we gave it a new name.
In the focusβ-rule,
how can we tell how much of the surrounding expression
is the predicate φ that is to become the sub-term of P?
For example, for F:ΣΣ,
| does F(φ(focusP)) reduce to F(Pφ) or to P(φ;F) ? |
So long as P is prime, it doesn’t matter, because these terms are equal. In Remark 11.4 we consider briefly what happens if this side-condition is violated.
Proof The double transpose H:ΣX→ΣΓ of P is a homomorphism with respect to the double transpose J:Σ→ΣΓ of F. ▫
The interaction of focus with substitution, i.e. cut elimination, brings no surprises.
Lemma 8.4 If Γ⊢ P:Σ2 X is prime
then so is Δ⊢ (u*P):Σ2 X for any substitution
u:Δ→Γ [Tay99, Section 4.3], and then
| Δ ⊢ u*(focusP) = focus(u*P) :X. |
Proof In the context [Δ, F:Σ3 X], since x, φ and F don’t depend on Γ,
| F(u*P) ≡ u*(F P) = u*(P(λ x.F(λφ.φ x))) ≡ (u*P)(λ x.F(λφ.φ x)), |
so u*P is prime. Then, in the context [Δ, φ:ΣX],
| φ(u*(focusP)) ≡ u*(φ(focusP)) = u*(Pφ) ≡ (u*P)φ = φ(focus(u*P)) |
using the focusβ-rule, whence the substitution equation follows by T0. ▫
Theorem 8.5 SC is a model of the sober λ-calculus.
Proof Since SC has products and powers of Σ (Proposition 6.11 and Corollary 7.2), it is a model of the restricted λ-calculus. Lemma 7.5 provides the interpretation of focusP and (the second form of) its β- and η-rules. ▫
Remark 8.6
Let C and D be the categories corresponding to
the restricted and sober λ-calculi respectively,
as in Remark 2.7.
Since the calculi have the same types, and so contexts,
D has the same objects as C and SC.
We have shown how to interpret focus in SC, and that the equations are valid there. Hence we have the interpretation functor ⟦−⟧:D→SC in the same way as in Proposition 2.8, where ⟦−⟧ acts as the identity on objects (contexts).
Since D interprets focus by definition, all of the objects of D are sober by Corollary 4.12. The universal property of SC (Theorem 7.6) then provides the inverse of the functor ⟦−⟧, making it an isomorphism of categories.
Alternatively, we can show directly that D has the same morphisms as SC, by proving a normalisation result for the sober λ-calculus. Besides being more familiar, this approach demonstrates that we have stated all of the necessary equations in the new calculus. We have already shown that the new calculus is a sound notation for morphisms of the category SC, and it remains to show that this notation is complete.
We can easily extract any sub-term focusP from a term of power type:
Lemma 8.7 φ[focusP] ⇔ P(λ x.φ[x]).
Proof [focusP/x]*φ[x] ⇔ (λ x. φ[x])(focusP), where [ ]* denotes substitution. ▫
The term φ in focusβ may itself be of the form focusP:
Lemma 8.8
Let Γ⊢ P:Σ3 X (sic) and Γ⊢ Q:Σ2 X
be primes. Then
| (focusP)(focusQ) ⇔ P Q and focusP = λ x.P(λφ.φ x). |
This equation for focusP is the one in Proposition 4.9 and Lemma 7.1.
Proof (focusP)(focusQ)=Q(focusP) ⇔ P Q using focusβ twice.
In particular, put Q=ηX(x)=λφ.φ x, so x=focusQ. Then
| (focusP)x = (focusP)(focusQ) ⇔ P Q ⇔ P(λφ.φ x), |
from which the result follows by the λη-rule. ▫
For the extra structure, we need a symbolic analogue of Proposition 7.9, now including the parameters Γ and m:ℕ. Note that S here is the double transpose of the same letter there.
Lemma 8.9 Let
Γ ⊢ Z:Σ2 X and
Γ, m:ℕ,u:X ⊢ S(m,u):Σ2 X be prime.
Put
|
Then Rn is prime and Γ, n:ℕ ⊢ rn=focusRn.
[This proof requires equational hypotheses in the context: see Remark E 2.7.]
Proof We prove
| Γ, n:ℕ ⊢ Rn = λ φ.φ(rn) |
by induction on n. For n=0, since Z is prime,
| λφ.φ(r0) = λφ.φ(focusZ) = λφ.Zφ = Z = R0. |
Suppose that Rn = λ φ.φ(rn) for some particular n. Then
|
Since Rn is equal to some λφ.φ(a), it is prime, and the required equation follows by focusη. ▫
Proposition 8.10
Every term Γ⊢ a:X in the sober λ-calculus
is provably equal (in that calculus) to
Cf. Lemmas 7.1 and 1 respectively.
Proof By structural recursion on the term a.
| ((focusP)=ℕ(focusQ)) may be rewritten as P(λ x.Q(λ y.x=ℕy)), |
Warning 8.11 Once again, this dramatic simplification of the calculus
(that focus is only needed at base types such as ℕ)
relies heavily on the restriction on the introduction of focusP
for primes only, i.e. on working in SC.
Hayo Thielecke shows that force is needed at all types
in the larger category HC whose morphisms involve control operators
[Thi97a, Section 6.5].
Theorem 8.12 If C is the category generated by
the restricted λ-calculus in Definition 2.1
then SC is the category generated by the sober λ-calculus.
If C has the extra structure in Remarks 2.4ff
then so does SC.
So the extension of the type theory is equivalent to the extension of the category.
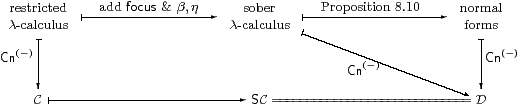
Proof We rely on the construction of the category Cn of contexts and substitutions developed in [Tay99], and have to show that the trapezium commutes.
The categories C, SC and D in Remark 8.6 have the same objects. The morphisms of C and D are generated by weakenings and cuts, where weakenings are just product projections. A cut [a/x]:Γ→Γ× X splits the associated product projection, and corresponds to a term Γ⊢ a:X in the appropriate calculus, modulo its equations.
By Proposition 8.10, the term a of the sober calculus is uniquely of the form focusP, where P is a prime defined in the restricted calculus (so the triangle commutes). Hence [a/x] in D corresponds to the SC-morphism <id,H>, where H is the double exponential transpose of P. ▫


