F:ΣY→ΣX, cf. Remark 3.13, and
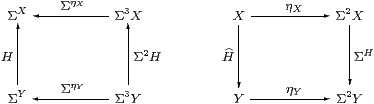
Thielecke and Führmann call these thunkable morphisms, since they write thunkX for ηX considered as an HC-map. It follows immediately (given Theorem 3.10) that ηX:X→ΣΣX is natural in SC but not HC.



Now we turn from the analysis to the synthesis of categories that have all objects sober. So our primary interest shifts from locales to the restricted λ-calculus in Remark 2.1.
Since we handle continuous functions f:X→ Y in terms of the corresponding inverse image maps Σf, it is natural to work in a category in which there are both “first class” maps f:X→ Y (given concretely by homomorphisms Σf:ΣY→ΣX) and “second class” maps F:X−× Y that are specified by any F:ΣY→ΣX.
These second class maps — ordinary functions rather than homomorphisms between algebras — are just what is needed to talk about U-split (co)equalisers as in Beck’s theorem (cf. Proposition 4.9 and [B]). Even in more traditional subjects such as group and ring theory, we do indeed sometimes need to talk about functions between algebras that are not necessarily homomorphisms.
The practical reason for according these maps a public definition is that the product functor is defined for them (Proposition 6.5), and this will be crucial for constructing the product of formal Σ-split subspaces in [B]. After I had hesitated on this point myself, it was seeing the work of Hayo Thielecke [Thi97b] and Carsten Führmann [Füh99] on continuations that persuaded me that this is the best technical setting, and this section essentially describes their construction.
As to the first class maps, the whole point of sobriety is that they consist not only of f:X→ Y in C, but other maps suitably defined in terms of the topology.
Definition 6.1
The categories HC and SC both have the same objects as C, but
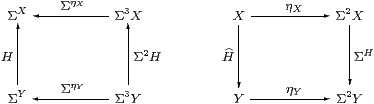
Thielecke and Führmann call these thunkable morphisms, since they write thunkX for ηX considered as an HC-map. It follows immediately (given Theorem 3.10) that ηX:X→ΣΣX is natural in SC but not HC.
Identity and composition are inherited in the obvious way from C, though contravariantly, which is why we need the F notation (which [Sel01, Section 2.9] also uses).
Remark 6.2 By Lemma 3.6, for f:X→ Y in C,
the map H=Σf:ΣY→ΣX is a homomorphism,
so H:X→ Y is in SC.
We shall just write this as f:X→ Y instead of Σf:X→ Y,
but beware that, in general,
different C-maps can become equal SC-maps with the same names.
By Remark 4.2, this functor C→SC is faithful iff every object of C is T0, and it also reflects invertibility if every object is replete. Theorem 4.10 said that it is also full iff every object of C is sober; as SC and C have the same objects, they are then isomorphic categories.
There are, of course, many more morphisms in HC than in C, but one (family) in particular generates the rest. We shall see that the new second class morphism force:Σ2 X−× X objectifies the operation P↦focusP that is only defined when P:Σ2 X is prime. Thielecke and Führmann apply their β-rule for force without restriction, producing computational effects, whilst our side-condition on focus gives it its denotational or topological meaning.
Definition 6.3
forceX = ηΣX : ΣΣX −× X
is a natural transformation in the category HC,
and satisfies ηX;forceX=idX or force(thunkx)=x.
Proof This is Lemma 2.10 again. force(−) in HC is ηΣ(−) in C, which is natural (in C) with respect to all maps F:ΣY→ΣX, so force(−) is natural (in HC) with respect to F:X−× Y. The other equation is ηΣX;ΣηX=idX. ▫
Corollary 6.4
The C-map ηX:X→Σ2 X is mono in both HC and SC.
Proof It is split mono in HC, and remains mono in SC because there are fewer pairs of incoming maps to test the definition of mono. ▫
Proposition 6.5 For each object X,
the product X×− in C extends to an endofunctor on HC.
This construction is natural with respect to C-maps
f:X→ Y (so H=Σf).
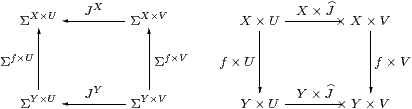
Proof For J:V−× U in HC, i.e. J:ΣU→ΣV in C, we write X× J:X× V−× X× U for the C-map JX:ΣX× U→ΣX× V. This construction preserves identities and composition because it is just the endofunctor (−)X defined on a subcategory of C. It extends the product functor because, in the case of a first class map g:V→ U (so J=Σg:ΣU→ΣV), we have X× J=X×Σg=ΣX× g=X× g, which is a first class map X× V→ X× U.
The construction is natural with respect to f:X→ Y because J(−) is. ▫
Example 6.6 The existential quantifier ∃ℕΓ in the context Γ
is obtained in this way,
and its Beck–Chevalley condition with respect to the substitution or cut
f:Γ→Δ
Proposition C 8.1 is commutativity of the square
(cf. Proposition 5.5):
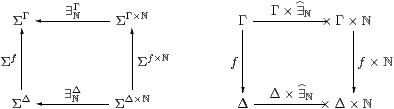
Example 6.7
× is not defined as a functor of two variables on HC,
because the squares

do not necessarily commute (+ [FS90]). For example, take F=J:Σ−×0 where F=J:Σ0=1→ΣΣ is the element ∼id∈ΣΣ; then these two composites give the elements ∼π0,∼π1∈ΣΣ×Σ.
Remark 6.8 × is a premonoidal structure
on HC in the sense of John Power [Pow02],
and a map F makes the square commute for all J
iff F is central (Definition 2).
Thielecke, Führmann and Selinger begin their development from HC
as a premonoidal category, whereas we have constructed it as
an intermediate stage on the journey from C to SC.
Definition 6.9
F:X−× Y is discardable or copyable
respectively if it respects the naturality of
the terminal (or product) projection (!) and the diagonal (Δ).
These terms are due to Hayo Thielecke [Thi97a, Definition 4.2.4], who demonstrated their computational meaning (op. cit., Chapter 6). In particular, non-terminating programs are not discardable, but he gave examples of programs involving control operators that are discardable but not copyable, so both of these properties are needed for a program to be free of control effects such as jumps (Remark 1.5). In fact, these conditions are enough to characterise first class maps in the topological interpretation [F], but not for general computational effects [Füh02]. [See the appendix to [F].]
Lemma 6.10 Δ is natural in SC,
i.e. all first class maps are copyable.
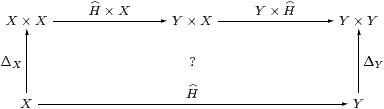
Proof As in Lemma 3.7, we show that the above diagram commutes by making it into a cube together with
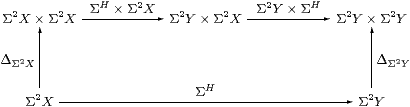
which commutes by naturality of Δ in C, as do the side faces of the cube, the other edges being ηX, ηX×ηY, etc. The top and bottom faces commute because H is a homomorphism and by naturality of H(−) and (Σ2 H)(−) with respect to ηX and ηY. The original diagram therefore commutes because ηY×ηY is mono by Corollary 6.4. ▫
Proposition 6.11
SC has finite products and C→SC preserves them.
Proof The terminal object 1 is preserved since Σ is the initial algebra (Lemma 3.12). The product projections and diagonals are inherited from C, so Δ;p0=id=Δ;p1 and Δ;(p0× p1)=id.
Then, for SC-maps a=H:Γ→ X and b=K:Γ→ Y, we obtain <a,b> as Δ;a× b, but we need centrality (Lemma 3.7) to make a× b well defined.
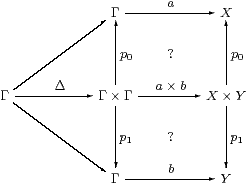
The issue is that the squares commute. In C, the upper one is
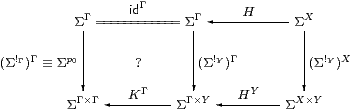
using one of the two definitions for H×K=a× b. The left-hand square commutes by Lemma 3.7 because K:ΣY→ΣΓ is discardable (as it is a homomorphism), and the right-hand square by naturality of H(−):ΣX×(−)→ΣΓ×(−) with respect to !:Y→1.
For uniqueness, suppose that f;p0=a and f;p1=b. Then
|


