


In this section we show how the abstract categorical and symbolic structures that we have introduced are equivalent to the traditional notions in general topology that we mentioned in Section 1. In fact, all that we need to do is to re-interpret lattice-theoretic work that was done in the 1970s. On this occasion our treatment will be entirely classical, making full use of the axiom of choice and excluded middle; for a more careful intuitionistic account see [B][C][G][H].
If you are not familiar with locally compact topological spaces, you may consider instead your favourite category of algebraic (or continuous) predomains, which are all sober. The discrete space ℕ is also needed, besides domains with ⊥. The results of this section are only used as motivation, so you can in fact omit it altogether.
Alternatively, the construction may be performed with arbitrary dcpos, although it adds extra points to those that are not sober. Peter Johnstone gave an example of such a non-sober dcpo [Joh82, Exercise II 1.9], as part of the philosophical argument against point-set topology. We shall not need this, as the localic view is already deeply embedded in our approach. In fact, when we construct new spaces in [B], they will be carved out as subspaces of lattices (cf. [Sco72]) not glued together from points.
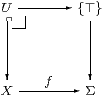
Remark 5.1 The classical Sierpiński space Σ has two points:
⊤ is open and ⊥ is closed. So altogether there are
three open sets: ∅, {⊤} and Σ.

This space has the (universal) property that, for any open subset U of any space X, there is a unique continuous function f:X→Σ such that the inverse image f*⊤ is U. Indeed, f takes the points of U to ⊤, and those of its closed complement to ⊥.
This is the same as the defining property of the subobject classifier Ω in a topos, except that there U⊂ X can be any subobject. We shall discuss sobriety for sets, discrete spaces and objects of a topos in Section 9.
Hence open subsets of X correspond bijectively to maps X→Σ, and so to points of the exponential ΣX. In other words, the space ΣX is the lattice of open subsets of X, equipped with some topology.
Remark 5.2 Finite intersections and arbitrary unions of open subsets
give rise to internal lattice structure on Σ, written
∧:Σ×Σ→Σ and ⋁:ΣU→Σ.
Besides the infinite distributive law,
conjunction also satisfies the Euclidean principle (Remark 2.4).
Whilst this is vacuous classically, it and its lattice dual
(which says that ⊥ classifies closed subsets)
capture remarkably much of the flavour of locale theory
[C][D],
before we need to invoke the continuity axiom (Remark 2.6),
though of course that is also valid in topology.
Remark 5.3 To determine the topology on the space ΣX,
consider the map ev:ΣX× X→Σ.
For this to be continuous,
Ralph Fox showed that the space X must be locally compact,
and ΣX must have the compact–open topology [Fox45],
which is the same as the Scott topology when we only consider Σ
and not more general target spaces.
The categorical analysis is due to John Isbell [Isb75].
Local compactness is a very familiar notion for Hausdorff spaces, but there are messy subtleties to its definition for non-Hausdorff spaces [HM81]. However, so long as we only consider spaces that are sober in the standard topological sense, things are not too difficult:
For any point x and open subset x∈ U⊂ X, there must be a compact subset K and another open subset V with x∈ V⊂ K⊂ U. The “open rectangle” around (U,x)∈ev−1{⊤}⊂ΣX× X that we need for continuity of ev is then
{W∈ΣX ∣ K⊂ W}× V ⊂ ΣX× X.
In the jargon, X has a base of compact neighbourhoods, cf. Bourbaki’s usage in Remark 1.8.
All of this is much prettier in terms of the open sets: the topology ΣX is a distributive continuous lattice, equipped with the Scott topology. Such a lattice is of course a frame, and the corresponding locale is called locally compact. Assuming the axiom of choice, the category LKLoc of locally compact locales is equivalent to the category LKSp of locally compact sober spaces [Joh82, Section VII 4.5].
Remark 5.4 Since ΣX carries the Scott topology,
a continuous function ΣY→ΣX
is a function between open set lattices that preserves directed unions.
Such a function is called Scott-continuous.
In particular, it preserves the order that is induced by the lattice structure
[Sco72].
Besides frame homomorphisms themselves, functions like this between frames do arise in general topology. For example, a space K is compact iff Σ!K:Σ→ΣK has a Scott-continuous right adjoint, ⋀:ΣK→Σ. Unfortunately, monotone functions between frames that need not preserve directed joins are also used in general topology, and these present the main difficulty that abstract Stone duality faces in re-formulating the subject [D].
Proposition 5.5
Let H:ΣX→ΣU be a Scott-continuous function
between the topologies of locally compact spaces.
If H is central (Definition 2) then it
preserves finite meets and arbitrary joins.
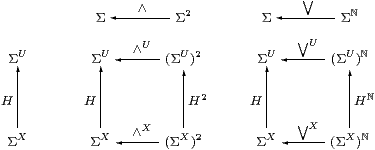
Proof Lemma 3.9 dealt with the constants (⊤ and ⊥), so consider J=∧:Σ2→Σ and ⋁:Σℕ→Σ. ▫
Remark 5.6 We also have ⋁:ΣU→Σ for any space U,
together with the associated distributive law.
In the case of U=ℕ, we write ∃ for ⋁,
and distributivity is known as the Frobenius law,
| ψ∧∃ n.φ(n) = ∃ n.ψ∧φ(n). |
We have ⋀:ΣK→Σ only when K is compact; in particular, it would be ∀ for K=ℕ, but (ℕ is not a compact space and) ∀ℕ is not computable (cf. Definition 1.3). Indeed, in a constructive setting, ⋁:ΣU→Σ only exists for certain spaces U, which are called overt (Section C 8). Overtness is analogous to recursive enumerability, cf. Remark 9.12 and Lemma 10.2.
We are now ready to show how our new λ-calculus formulation in Sections 3–4 captures the hitherto lattice-theoretic ideas of continuous functions and sober spaces. A proof entirely within abstract Stone duality (including the continuity axiom) that preserving the lattice operations suffices will be given in Theorem G 10.2.
Theorem 5.7
Let U and X be locally compact sober spaces and
H:ΣX→ΣU a Scott-continuous function between their topologies.
Then the following are equivalent:
Proof We have just shown that central maps are frame homomorphisms.
Since X is sober in the topological sense, all frame homomorphisms ΣX→ΣU are of the form Σf for some unique f:U→ X (we take this as the topological definition of sobriety). But all Σf are Eilenberg–Moore homomorphisms. ▫
Corollary 5.8 The following are equivalent for
P:1→ΣΣX:
Similarly, for a continuous function P:U→ΣΣX, the same equivalent conditions hold for P(u) for each point u∈ U. ▫
Remark 5.9 Our primes are therefore what Johnstone calls
the “points” of the locale ΣX,
so sobriety for LKSp in our sense agrees with his
[Joh82, Section II 1.6].
As a topological space, the equaliser is the set U of primes,
equipped with the sparsest locally compact topology
such that U→Σ2 X is continuous,
and the hom-frame C(X,Σ) provides this topology.
Remark 5.10
We have a theorem in the straightforward sense for LKSp
that says that, given a Scott-continuous map H:ΣX→ΣU
between the open-set lattices of given locally compact spaces,
H is a homomorphism of frames if and only if it is a homomorphism
in the sense of our monad.
By contrast, the notions of sobriety expressed in terms of lattice theory and the λ-calculus agree only in intuition. We are only able to bring these two mathematical systems together in a setting where topological sobriety has already been assumed. If you are skeptical of the mathematical status of the argument, consider the analogous question in the relationship between locales and Bourbakian spaces: at what point in the axiomatisation of locales do we make the assumption that renders them all sober? Even then, these two categories only agree on their products on the same subcategory as ours, namely locally compact spaces. In summary, the concordance of several approaches (along with [G], and models of synthetic domain theory [Tay91]) makes us confident that the notion of locally compact space is a good one, but not so sure how it ought to be generalised.
Remark 5.11 The types of the restricted λ-calculus,
even with the additional lattice and recursive structure,
form a very impoverished category of spaces.
Identifying them with their interpretations in LKSp,
they amount merely to (some of) the algebraic lattices
that Dana Scott used in the earliest versions of his denotational semantics
[Sco76],
and include no spaces at all (apart from 1 and ℕ)
that would be recognisable to a geometric topologist.
The monadic property populates the category of spaces with subspaces of the types of the restricted λ-calculus. We show how to do this in terms of both abstract category theory and as an extension of the λ-calculus similar to the axiom of comprehension in [B], which also proves the next result intuitionistically for locales.
Although we only intended to consider sobriety and not monadicity in this paper, we actually already have enough tools to characterise the algebras for the monad classically in lattice-theoretic terms. Further proofs appear in [B][G][H].
Proof As all of the spaces are sober, the functor in Definition 4.1 is full and faithful. It remains to show that every Eilenberg–Moore algebra (A,α) is of the form (ΣX,ΣηX) for some locally compact space X. But, as A is a retract of a power of Σ, it must be a continuous lattice equipped with the Scott topology, and must in fact also be distributive, so A≅ΣX for some locally compact sober space X.
However, we still need to show that the Eilenberg–Moore structure α:Σ2 A→ A is uniquely determined by the order on A, and is therefore ΣηX as in Lemma 3.3.
For this, we must determine α F for each element F∈Σ2 A; such F defines a Scott-open subset of the lattice ΣA. It can be expressed as a union of Scott-open filters in this lattice, i.e. these filters form a base for the Scott topology [Joh82, Lemma VII 2.5] [GHK++80, Section I.3]. Since α must preserve unions, it suffices to define α F when F is a Scott-open filter.
Now each Scott-open filter F itself corresponds to compact saturated subspace K⊂ A [HM81, Theorem 2.16], cf. Remark 1.10. For a lattice A with its Scott topology, a “saturated” subspace is simply an upper set. Since α must be monotone and satisfy ηA;α=idA, we have α(F)≤ a for all a∈ K. For the same reason, if b∈ A satisfies ∀ a. a∈ K⇒ b≤ a then b≤α(K). Hence α(F)=⋀ K∈ A. Thus the effect of α on all elements of Σ2 A has been fixed, as a join of meets. ▫
Setting aside the discussion of more general spaces, what we learn from this is that, when all objects are sober, there are “second class” maps between objects. We shall see in the next section that this phenomenon arises for abstract reasons, and that the potential confusion over (Scott-) “continuous maps between frames” is not an accident.


