Sobriety and description

10 Sobriety and description

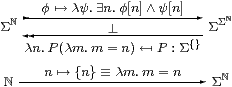
In this section we prove that focus and description are inter-definable, for the natural numbers. In the following notation, we need to show that φ is a description iff P is prime.

Lemma 10.1 This is a retraction,

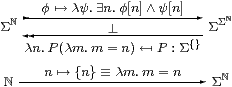
cf. the connection between {} and η in [BW85, Lemma 5.1.3] and Lemma C 6.12. ▫

[In fact there is an adjunction or coclosure as shown, since

P	↦	φ≡λ n.P(λ m.n=m)
	↦	λψ.∃ n.φ n∧ ψ n
	≡	λψ.∃ n.P(λ m.n=m)∧ ψ n
	=	λψ.∃ n.P(λ m.n=m∧ ψ n)
	≤	λψ.P(λ m.ψ m) ≡ P

using the Euclidean principle (Remark 2.4) and the substitution rule for equality.]

First, we characterise the image of Σ^ℕ↣Σ^{Σ^ℕ}.

Lemma 10.2 Γ⊢ P:Σ²ℕ is of the form λ ψ.∃ n.φ[n] ∧ ψ[n] for some Γ⊢φ:Σ^ℕ iff it preserves ∃_ℕ. In this case, φ=λ n.P(λ m.n=m).

Proof Suppose that P preserves ∃. Then

Pψ	⇔	P(λ m.∃ n.n=m∧ψ[n])
	⇔	∃ n. P(λ m.n=m∧ψ[n])
	⇔	∃ n. P(λ m.n=m)∧ψ[n]

by the Euclidean principle (Remark 2.4). The other way is easy. ▫

For the rest of this section, P and φ will be related in this way.

Lemma 10.3 P preserves ⊤ iff φ satisfies the existence condition, and P preserves ∧ iff φ satisfies the uniqueness condition.

Proof For the first, observe that P⊤ ⇔ ∃ n.φ[n]. For the second, if φ[n₁]∧ψ₁[n₁] and φ[n₂]∧ψ₂[n₂] then n₁=n₂=n by uniqueness. ▫

Proposition 10.4 If P is prime then φ is a description, and the n.φ[n] satisfies the rules for focusP (Definition 8.2).

Proof As P is prime, it preserves ⊤, ∧ and ∃ because its double exponential transpose is a homomorphism, in particular with respect to ⊤, ∧ and ∃, as in Proposition 5.5. Also, P=λψ.∃ n.φ[n]∧ψ[n] by the Lemma, so Pψ⇔ψ[the n.φ[n]], which means that the β-rules agree. For the η-rules,

φ=

⎧
⎨
⎩

⎫
⎬
⎭

≡(λ m.m=n) iff P=thunkn≡λψ.ψ[n],

which are respectively a description and prime, and then (the m.φ[m])=(focusP)=n. ▫

Corollary 10.5 Any overt discrete object that admits definition by description is sober. In particular, all sets and all objects of any topos are sober. ▫

The converse is the case X=ℕ of Theorem 5.7, that if H:Σ^ℕ→Σ^U is a frame homomorphism (i.e. it preserves ⊤, ∧ and ∃) then it is an Eilenberg–Moore homomorphism. Of course, we showed that for LKLoc, by re-interpreting results from the literature, not for our abstract calculus. The proof below depends on (primitive) recursion, so only applies to ℕ rather than to discrete overt spaces in general, although when the whole theory is in place the result will hold for them too. [It is easy to show that if φ is a description then P preserves ⊤, ⊥, ∧ and ∨; then it is prime by Theorem G 10.2.]

But before considering ℕ we have to deal with 2≡{0,1}. As we did not ask for this as a base type in Section 2, ψ:Σ² may be replaced by <ψ₀,ψ₁>∈Σ×Σ, and similarly for the type of P. (Alternatively, one could formulate a result with ψ:Σ^ℕ to capture the same point.) See B 11 for further discussion of disjoint unions in abstract Stone duality.

Proposition 10.6 Let α:Σ be decidable, with β⇔¬α (Definition 9.11). Then

P ≡ λψ.(α∧ψ[0])∨(β∧ψ[1])

is prime. This justifies definition by cases: (if α then 0 else 1)≡focusP.

Proof Let P_αβ be the obvious generalisation, so

γ∧ P_αβ = P_{(γ∧α)(γ∧β)}

by distributivity. The equation that we have to prove for Definition 8.1 may be written

(α∨β)∧F P_αβ ⇔ (α∧F P_⊤⊥) ∨ (β∧F P_⊥⊤).

By the Euclidean principle (Remark 2.4) and the lattice laws, we have

α∧F P_αβ	⇔	α∧F(α∧ P_αβ)
	⇔	α∧F(α∧ P_α(α∧β))
	⇔	α∧F(α∧ P_α⊥)
	⇔	α∧F(α∧ P_⊤⊥)
	⇔	α∧F P_⊤⊥ ▫

Lemma 10.7 For any description φ, we define, by primitive recursion,

φ^≥[0]≡⊤ φ^>[n]≡φ^≥[n+1]≡φ^≥[n]∧¬φ[n]

φ^<[0]≡⊥ φ^≤[n]≡φ^<[n+1]≡φ^<[n]∨φ[n].

Then φ^<[n] has the properties of the ordinary arithmetic order, that is, (the m.φ[m])< n, and similarly for the others. ▫

Proposition 10.8 If φ is a description then P is prime, and focusP satisfies the rules for the n.φ[n].

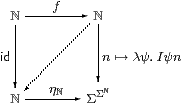
Proof The idea of the proof is to define a permutation f:ℕ≅ℕ that cycles the witness to 0 and any smaller values up by 1, leaving bigger numbers alone. The function f itself is defined by (cases and) primitive recursion, but it only has an inverse with general recursion. Let

f(n) ≡

⎧
⎪
⎨
⎪
⎩

0	if φ[n]
n	if φ^<[n]
n+1	if φ^>[n]

δ(n,m) ≡

⎧
⎪
⎨
⎪
⎩

	m=0	∧	φ[n]
∨	m=n	∧	φ^<[n]
∨	m=n+1	∧	φ^>[n],

so δ(n,m) ⇔ f(n)=m. The operations Σ^f and I, defined by

Σ^fθ	≡	λ n.∃ m.δ(m,n)∧θ[m]
Iψ	≡	λ m.∃ n.δ(m,n)∧ψ[n],

are mutually inverse, because, by expanding disjunctions,

∃ m.δ(m,n)	⇔	φ[n]∨φ^<[n]∨φ^≥[n+1]
∃ n.δ(m,n)	⇔	(m=0∧∃ n.φ[n])∨(∃ n.m=n+1)
δ(m,n₁)∧δ(m,n₂)	⇔	(n₁=n₂)∨(φ^<[m]∧φ^>[m])
δ(m₁,n)∧δ(m₂,n)	⇔	(m₁=m₂)∨(φ[n]∧φ^<[n])∨ (φ[n]∧φ^>[n+1]).

Thus Σ^f is a homomorphism, as is its inverse I by Proposition 3.5. But so too is evaluation at 0, so

ψ ↦ θ[0] ≡ ∃ n.δ(0,n) ≡ ∃ n.φ[n]∧ψ[n]

is a homomorphism, and P is prime. The β- and η-rules agree as before. ▫

Remark 10.9 Sobriety says that the functor Σ⁽⁻⁾:C^op→A in Definition 4.1 is full and faithful. But in this proof we only used the fact that it reflects invertibility, so it suffices to assume that ℕ is replete. Then f⁻¹ is the diagonal mediator that is provided by the orthogonality property [Hyl91, Tay91].

Corollary 10.10 H:Σ^ℕ→Σ^U is an Eilenberg–Moore homomorphism iff it preserves ⊤, ∧ and ∃. ▫

This result can be extended from ℕ to higher types on the assumption of the continuity axiom (Remark 2.6). Hence there is a version of Theorem 5.7 that links the notions of homomorphism and sobriety that we have introduced entirely abstractly using the λ-calculus with those that arise from the ℕ-indexed lattice structure in Remarks 2.4ff. Although the proof would only require one more section, it begins to make serious use of domain-theoretic ideas, and so properly belongs in a discussion of that subject [F][G]. Besides, surprisingly much progress can be made with the development of topology without the extra axiom.