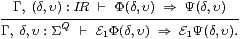



You might reasonably expect that our next task would be to construct R as an object of ASD. This would involve showing that the formula E in Section 2 satisfies the definition of a nucleus in Section 5, and that its admissible terms are exactly the Dedekind cuts of Section 6.
However, hard experience with nuclei has shown that one cannot go at them like a bull in a china shop: whilst the calculations are elementary, they are very tricky. In fact, it is precisely because we want to give an elementary proof (in the technical sense of the word, i.e. in a very weak logic) that it is difficult. If we were willing to assume all of the structure of set theory, Proposition 2.17 for ℝ would already have justified the equations in Lemma 5.4. The elementary proof requires messy manipulation of sequences of rationals.
Sorting out the mess teaches us two things conceptually.
One is that we need to construct the ascending and descending reals and the interval domain first. The other is that the Euclidean nucleus E turns out to be a composite of four parts that are examples of the easy ways of defining nuclei in ASD, namely idempotents, open subspaces, closed subspaces and Scott-continuous localic nuclei (Definition 5.5 and Lemma 5.9). As we shall also see with arithmetic, the interval domain collects the “easy” properties of real numbers, clearing the ground for work on the difficult property of locatedness.
The technical difficulties that we resolve in this section may seem to be of our own making, as we have allowed δ,υ:ΣQ to be arbitrary λ-terms of this type. These terms may, for example, pick out individual rationals for “special” treatment, in the way that we find in the pathological counterexamples of real analysis but not its fundamental intuitions. As we explained in Remark 2.13, we start from ΣQ because that is as close to computation as is reasonable, whereas the other structures are partial compromises with mathematics. (The order and arithmetic on Q are complicated when encoded via the bijection Q≅ℕ, but are well known to lie within a weak fragment of logic like ASD.) Also, the types in ASD must be defined progressively from 1 and ℕ using ×, Σ(−) and Σ-split subspaces, so we have to use ΣQ(≅Σℕ) on the way to constructing the interval domain and finally R.
We dispose of most of the arbitrariness by constructing the spaces of ascending and descending reals (Example 2.8) as retracts of ΣQ.
Notation 7.1
For arbitrary δ,υ:ΣQ and Φ:ΣΣQ×ΣQ, define
| d ≡ ∃ e. (d< e) ∧ δ e, |
| u ≡ ∃ t. υ t∧ (t< u), |
| B(δ,υ) ≡ ∃ d u.δ d∧υ u, ∇(δ,υ) ≡ ∃ d u.δ d∧(u< d)∧υ u |
and
| E1Φ(δ,υ) ≡ ∃ d< u. |
| d∧ |
| u∧Φ(δd,υu). |
As the name “roundedness” suggests, δ and υ trim off the endpoints of cuts of the kind that Dedekind originally introduced, cf. Remark 2.1, as well as closing the subsets down- or upwards. The predicates B and ∇ capture boundedness and (non-)disjointness respectively (note the u< d in ∇!). We shall find three nuclei that define the interval domain, but E1 will turn out to be the most useful one.
Lemma 7.2
These operations δ↦δ and υ↦υ
are idempotent.
They fix δ and υ iff these are rounded
(Definition 6.8).
In particular, δd, ⊤ and ⊥ are fixed by the first
operation (rounding downwards),
whilst υu, ⊤ and ⊥ are fixed by the second (upwards). ▫
Definition 7.3
Using Lemma 5.9, these idempotents on ΣQ define types
| : |
| ◁ΣQ and |
| : |
| ◁ΣQ, |
called the ascending and descending reals respectively. The product R×R is similarly a retract of ΣQ×ΣQ, so it is given by the nucleus
| Er Φ(δ,υ) ≡ Φ( |
| , |
| ) ≡ Φ(λ d.∃ e. d< e ∧ δ e, λ u.∃ t. υ t∧ t< u). |
We may think of the lattice R×R as the space of “intervals” that may be infinite and even back-to-front (Remark 2.20).
Lemma 6.12 defines “inclusion” maps δ(−):Q→R◁ΣQ and υ(−):Q→R◁ΣQ. These can be extended to R→R and R→R, of course simply as the projections that extract δ and υ from the cut (δ,υ):R. However, by monotonicity (Axiom 4.8), there is no map
| → |
| , |
| → |
| , |
| → R or |
| → R |
that commutes with these inclusions. This is why both δ and υ are needed in the definition of Dedekind cuts.
Exercise 7.4 Construct the ascending natural numbers, with ∞ as top,
in a similar way.
Next we consider disjointness. Of the three possible definitions, in Definition 6.8 we chose the one that is invariant under rounding, so that the nuclei commute, cf. Lemma 5.11.
Lemma 7.5 Let δ,υ:ΣQ.
Then ∇(δ,υ)⇔∇(δ,υ)
and E1∇(δ,υ)⇔⊥.
Also, the statements (a,d,e,f) below are equivalent:
|
However, if Q is discrete then δ≡λ d.(d≤ r) and υ≡λ u.(r≤ u) satisfy (a,d,e,f) but not (b,c); in fact (b) is equivalent to (a&c).
Proof
|
Definition 7.6
The unbounded interval domain is the closed subspace
IR∞⊂R×R that is co-classified
by ∇, so it consists of those (δ,υ)
for which ∇(δ,υ) is false (Remark 4.11),
i.e. which are rounded and disjoint.
Using Lemma 5.9, IR∞⊂ΣQ×ΣQ
is defined by the nucleus
| Erd Φ(δ,υ) ≡ ∇( |
| , |
| )∨Φ( |
| , |
| ). |
The inclusion map IR∞→R×R provides the endpoints of any interval, but as ascending and descending reals: there is no such map IR∞→ R× R (cf. Remark 2.9). On the other hand, there is of course a function from {(d,u) ∣ d≤ u}◁ R× R to IR∞ that provides the interval with specified endpoints.
That version of the interval domain included (⊥,υu)≡[−∞,u], (δd,⊥)≡[d,+∞] and (⊥,⊥)≡[−∞,+∞]. The following construction, on the other hand, eliminates them; since it therefore has no least element, it is called a predomain. It is again invariant under rounding.
Lemma 7.7 ∇(δ,υ)=⇒
B(δ,υ) ⇔ B(δ,υ) ⇔ E1⊤(δ,υ).
Proof
|
Definition 7.8
The bounded interval predomain is the open subspace
IR⊂ IR∞ classified by B,
so it consists of those (δ,υ)
for which B(δ,υ) is true.
By Lemma 5.9, IR⊂ΣQ×ΣQ
is defined by the nucleus
| Erdb Φ(δ,υ) ≡ ∇( |
| , |
| )∨Φ( |
| , |
| )∧ B( |
| , |
| ), |
which may be bracketed either way, since ∇⊑ B.
Warning 7.9 Here we are selecting the bounded pseudo-cuts from
spaces of not necessarily bounded ones.
Nuclei that do this do not preserve ⊤.
This is related, via Lemma 5.13,
to the fact that [d,u] is compact, but R is not.
The following rule of inference will simplify matters a lot in the next section. Abstractly, it is just (monotonicity of) the I operator in Section 5 for the subspace IR⊂ΣQ×ΣQ.
Proposition 7.10 In proving any implication Φ⊑Ψ,
we may assume that the pseudo-cuts to which they are applied
are rounded, bounded and disjoint
(or even that they have rational endpoints),
at the cost of applying E1 to the result, in the sense that
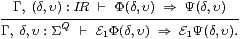
|
Proof If d< u then (δd,υu) is rounded, bounded and disjoint, so
|
Exercise 7.11 Use the following result to sharpen this rule to show that
the premise
| Γ, q:Q ⊢ Φ(δq,υq) ⇒ Ψ(δq,υq) |
is sufficient to deduce E1Φ⊑E1Ψ, and indeed EΦ⊑EΨ, as we shall see in the next section. ▫
Next we invoke Scott continuity of Φ, cf. Lemma 2.16.
Proposition 7.12 If (δ,υ) are rounded and bounded
then, for any Φ:ΣΣQ×ΣQ,
| Φ(δ,υ) ⇔ ∃ d u. δ d∧υ u∧ Φ(δd,υu). |
If (δ,υ) are also disjoint then Φ(δ,υ) ⇔ ∃ d< u. δ d∧υ u∧ Φ(δd,υu) ≡ E1Φ(δ,υ).
Proof We have to show that the joins in Notation 7.1,
| = ∃ d.δ d∧(λ x.x< d) and |
| = ∃ u.υ u∧ (λ x.u< x), |
are directed in the sense of Definition 4.20, so consider
| N ≡ Q, αd ≡ δ d and φd ≡ δd ≡ λ x.x< d. |
Then ∃ d.αd⇔⊤ by boundedness, and the binary operation @≡max satisfies
| αd@e ≡ δ(max(d,e)) ⇔ δ d∧δ e ≡ αd∧αe |
as δ is lower, and φd@e x ≡ x<max(d,e) ⇐= (x< d)∨(x< e) ≡ (φd∨φe)x.
For the second, we use @≡min instead.
Then we deduce the result for rounded and bounded
(δ,υ)=(δ,υ) from Axiom 4.21.
If they are also disjoint then δ d∧υ u⇒ d< u
by Lemma 7.5. ▫
It may perhaps be surprising that this is the (one) place where Scott continuity is used in the construction, given that the manipulation of finite lists will happen in the next section. The reason is that this is the section in which we do domain theory. The intervals with rational endpoints provide a basis for the domain of general intervals in the sense of Remark 2.9, and the Proposition shows how we extend the definition of Φ from the basis to the whole domain.
In fact, we have shown that there is at most one extension. We need another condition to ensure that the extension exists, i.e. that we recover the given formula when we restrict back to the basis. This requirement is more than monotonicity with respect to interval inclusions, since the bounded interval predomain is a continuous but not algebraic dcpo.
Proposition 7.13 Let φ(d,u) be any predicate
on d,u:Q, which are intended to be the endpoints of an interval. Then
| Φ(δ,υ) ≡ ∃ d u.δ d∧υ u∧φ(d,u) |
extends φ:Q× Q→Σ to Φ:ΣQ×ΣQ→Σ, in the sense that Φ(δd,υu)⇔φ(d,u), iff
| φ is rounded, φ(e,t) ⇔ ∃ d u.(d< e)∧(t< u)∧φ(d,u). |
If φ satisfies the same condition in just the restricted case where d≤ u, then it extends to the bounded interval predomain, Φ:IR→Σ, i.e. to rounded, bounded, disjoint pseudo-cuts (δ,υ). ▫
We shall use this condition in the definition of the nucleus E in the next section, and again for arithmetic in Sections 11–13. Here we may complete the construction of the (bounded) interval (pre)domain in ASD:
Theorem 7.14 E1 is a nucleus (Definition 5.5), and
(δ,υ) is admissible for it (Definition 5.7)
iff it is rounded, bounded and disjoint, so IR≅{ΣΣQ×ΣQ ∣ E1}.
Proof If (δ,υ) are rounded, bounded and disjoint, Φ(δ,υ)⇔E1Φ(δ,υ) by Proposition 7.12, i.e. (δ,υ) is admissible. On the same hypothesis, therefore,
| (Φ∧Ψ)(δ,υ) ⇔ (E1Φ∧E1Ψ)(δ,υ). |
We deduce from this, using Proposition 7.10, that, for arbitrary (δ,υ),
| E1(Φ∧Ψ)(δ,υ) ⇔ E1(E1Φ∧E1Ψ)(δ,υ), |
which was one of the equations for a nucleus. We can prove the ∨-equation in the same way, or by observing that E1 is idempotent and preserves ∨.
Conversely, we have to deduce roundedness, boundedness and disjointness from instances of admissibility with respect to the new formula for E1, using carefully chosen Φ, which are provided by Lemmas 7.5 and 7.7.
For disjointness, let Φ≡∇, so by admissibility, ∇(δ,υ) ⇔ E1∇(δ,υ) ⇔ ⊥.
For boundedness, let Φ≡λαβ.⊤, so B(δ,υ) ⇔ E1Φ(δ,υ) ⇔ Φ(δ,υ) ⇔ ⊤.
For roundedness, consider Φ≡λαβ.α c∧β w with c,w:Q, so
|
since (δ,υ) are rounded and disjoint. By admissibility,
| δ c∧υ w ≡Φ(δ,υ) ⇔E1Φ(δ,υ) ⇔ |
| c∧ |
| w. ▫ |
We conclude by looking at two other nuclei that also define IR.
| Er Φ(δ,υ) ≡ Φ( |
| , |
| ), EdΦ≡Φ∨∇ and EbΦ≡Φ∧ B; |
| ErbΦ(δ,υ) ⇔ ∃ d u. |
| d∧ |
| u∧Φ(δd,υu) ⇔ ∃ e t.δ e∧υ t∧Φ(δe,υt) |
We prefer E1 because it preserves ⊥, whereas Erdb⊥=∇. We use this property in Theorem 9.2 to construct the existential quantifier. ▫
Exercise 7.16 Let
E1′Φ(δ,υ) ≡
∃ d< u.δ d∧υ u∧Φ(δd,υu)
and show that
We prefer E1 because it commutes with Er (cf. Lemma 5.11), so the Σ-splitting for IR↣ΣQ×ΣQ given by E1 restricts to IR↣R×R. ▫


