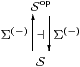



5.1. We do not require underlying sets for the category S,
because the new notion of “space” is intended to be an unknown.
However, algebras need carriers.
The fundamental idea of Abstract Stone Duality is
to use the (as yet, unknown) spaces as carriers for the algebras.
In particular, in topology, we regard the lattice of open subspaces
of a space as another space, following
another methodological principle due to Marshall Stone:
“always topologize” [Sto38].
For Stone equivalence, A≃Sop. So we are saying that we want Sop to be a category of algebras over S. For this, we need a way of formulating (potentially infinitary) algebraic theories that works over any category S and not just over the category of sets. Such an account is provided by the categorical notion of monad [Lin69]. The textbook on universal algebra using monads has, unfortunately, never been written, but [Man76] perhaps comes closest to it.
In §6 we shall give some of the formal definitions for monads, as adapted to ASD, and the full treatment is of course given in the papers cited. However, our purpose here is to tell the story behind these ideas.
5.2. Recall that concrete Stone dualities often arise from a “schizophrenic”
object Σ, i.e. one for which T X≡S(X,Σ).
On the other hand, by the new hypothesis, T X is also to be an object of S.
So it is natural to ask that S have all exponentials
of the form ΣX,
by which we mean that S-maps Γ× X→Σ
are to be in natural bijection with those Γ→ΣX
(§2.5).
A pre-requisite for this definition is that S have finite products,
1 and ×.
Note that we are asking just for powers of Σ
(and, consequently, of its powers too), but not of general objects.
In other words,
we are not saying that the category should be cartesian closed —
at least
at this stage,
cf. §12.9.
Nevertheless, any object Σ that has powers gives rise to an adjunction
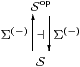
which we write vertically in order to avoid confusing it with the one in §4.2 for Stone duality.
This adjunction induces a monad on S, so let A be its category of Eilenberg–Moore algebras, for which the standard theory gives a comparison functor Sop→A [EM65] [Tay99, 7.5.3(c)]. Formulating abstract Stone duality as an axiom on S, we ask that this be an equivalence, cf. §4.7.
As we want to develop a formalism inspired by the λ- and predicate calculi (§2), and to get away from that of set theory, we shall use Greek letters (φ, ψ, θ) for terms of type ΣX, which will represent open subspaces. Then, instead of writing x∈ U for membership, we use λ-application, φ x. (We shall re-employ the set-theoretic notation for more general kinds of subspaces than open ones in §§6.7 & 12.8.)
5.3.
Before making things any more abstract, let’s link this idea back
to the concrete case of set theory instead of topology (cf. §2.10).
The Lindenbaum–Tarski theorem (§4.5) is strictly classical,
but Robert Paré proved a categorical version
of it that is valid any elementary topos S
or in any model of intuitionistic Zermelo set theory.
The powerset ℘(X) is given by the exponential ΩX,
where Ω is the lattice of truth values,
which we shall discuss further in §7.
Paré showed that the contravariant functor Ω(−) is monadic
in the above sense [Par74].
We find limits of algebras by computing them for their carriers and lifting the algebraic structure; in categorical jargon, the functor U :A→S creates limits. Since A≃Sop, this derives colimits in S from its limits. (Christian Mikkelsen had already shown this by other methods [Mik76].) These results simplified the definition of an elementary topos by removing the need to assert the existence of colimits as an axiom, as had been done previously.
5.4.
This result was also the original inspiration for ASD, in 1993,
although the results that we discuss in the rest of this section
were discovered much later.
How could we set up the monadic situation in topology, within the category of Bourbaki spaces? Ralph Fox’s original investigations [Fox45] showed that the function-space YX only behaves reasonably well when X is locally compact. The meaning of “reasonably well” crystalised into the notion of a cartesian closed category that emerged in the 1960s and was shown to be equivalent to the λ-calculus (§§2.2 & 2.5). It was meanwhile becoming clear that the filter of open neighbourhoods of a compact subspace (§5.7) plays a more important role than its set of points [Wil70].
Then Dana Scott [Sco72] saw that the crucial case is the function-space ΣX, where Σ is the Sierpiński space (§7). ΣX is the lattice of open subsets of X, but it obeys the universal property in §2.5 iff X is locally compact and ΣX has the non-Hausdorff topology that now bears Scott’s name. The study of continuous lattices [GHK++80] and domain theory grew out of this. For a historical study of function spaces in topology, see [Isb86].
The category of locally compact spaces has products and an object Σ that has powers ΣX, as we require. Whilst general functions-spaces YX exist as Bourbaki spaces when X is locally compact, the result need no longer be locally compact, so we do not have a cartesian closed category. In particular, ℕℕ, known as Baire space, is not locally compact, essentially because its open subspaces are rather large, whilst its compact ones are rather small.
Nevertheless, cutting down to sober spaces, we have a model of the monadic situation above, as we show in §§5.8ff.
5.5.
Category theory is a very potent drug, which should only be prescribed
in small quantities.
A theorem of Jon Beck [Tay99, §7.5]
(he never published it himself)
characterises when an adjunction F ⊣ U is monadic
in terms of two properties of the right adjoint U:A→S:
First, U must reflect invertibility: for f:A→ B in A, if U f has an inverse in S then f already had one in A. We shall see in §6.2 that this is equivalent to our abstract definition of sobriety.
Second, U must create U -split coequalisers (cf. §5.3). New students balk at this clause, but it is the active ingredient in this categorical medicine. We need to explain Σ-split equalisers, which the coequalisers become under the contravariance. These are subspaces i:S⊂ X that have the subspace topology, i.e. any open subspace of S is the restriction of one of X, but in a canonical way. That is, there is a map I:ΣS→ΣX for which Σi· I=idΣS.
Beck’s theorem says that, given an idempotent E on ΣX that ought to define a Σ-split subspace of X, then it does: there are i and I for which E=I·Σi. We shall give the formal definitions in §6.5.
5.6.
The simplest (and first, [C]) examples of
Σ-split subspaces are open and closed ones.
Any open subsubspace V⊂ U⊂ X of an open subspace is already an open subspace of X. Conversely, the inverse image of W⊂ X in U is the intersection, U∩ W. Then the operation U∩(−) provides Σi:ΣX→ΣU for the inclusion i:U⊂ X, and its splitting I:ΣU→ΣX is the inclusion (V⊂ U)↦(V⊂ X). The composite E≡ I·Σi is the idempotent U∩(−) on ΣX. In the ASD notation, U and V are represented by their classifiers θ and φ, and then E is λφ.φ∧θ.
In the case of closed subspaces, any open subsubspace V⊂ C⊂ X is also the intersection with C of some open subspace of X. But in this case the most convenient choice of representative is the maximal one, V∪ U, where U is the open complement of C. This provides I, whilst Σi is represented by U∪(−). Now E≡ I·Σi is U∪(−) or λφ.φ∨θ on ΣX.
5.7.
Before giving further examples of Σ-split subspaces,
we need to say something about compact ones.
Recall that a subspace K⊂ X of a Bourbaki space is compact if,
whenever K⊂⋃i Ui for some family of open subspaces,
this already holds for some finite subfamily.
This says exactly that the predicate K⊂ U is Scott continuous
as U ranges over open subspaces of X.
The result lies in the object of truth values,
considered as a topological space,
so the predicate is a continuous function A:ΣX→Σ.
The operator A obeys the Gentzen-style rule (cf. §2.1) for universal quantification of any predicate φ over K, so long as φ denotes an open subspace:
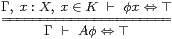
|
In particular, if K=X then A is the universal quantifier ∀, whilst if it is a subspace we sometimes write A as a modal operator ▫, which we read as “must” or “necessarily”. We explain in §12 why we use a symbol ∀ instead of ∀.
5.8.
We can show how the definitions of local compactness
for Bourbaki spaces and locales
express the object in question as a Σ-split subspace of ΣN,
where N is any set, which we may think of as ℕ or a cardinal.
Then ΣN is the powerset of N,
or the topology on N considered as a discrete space,
where ΣN is itself equipped with the Scott topology.
According to the definition for not necessarily Hausdorff spaces given in [HM81], if a point lies in an open subspace (x∈ U) then there is a compact subspace K and an open one V such that x∈ V⊂ K⊂ U. Moreover, the space has a family of such pairs (Vn,Kn), indexed by a set N.
Now let An:ΣX→Σ or An:ΣΣX be the Scott-continuous operator corresponding to the subspace Kn, for each index n∈ℕ. The open subspaces U and Vn are represented in our notation by φ,βn:ΣX. (We use super- and subscripts to indicate whether these subspaces or terms increase or decrease as the index n:N increases.)
Hence local compactness says that
| U = ⋃ {Vn ∣ Kn⊂ U} or φ = ∃ n. βn∧ Anφ, |
which we call the basis decomposition. Then the maps i:X→ΣN and I:ΣX→ΣΣN, defined by
| i x ≡ λ n.βn x and Iφ ≡ λξ.∃ n.ξ n∧ Anφ, |
satisfy Σi· I=idΣX.
5.9.
A locally compact locale is one whose corresponding frame
is a continuous lattice [Joh82, §VII 4].
This relativises the notion of compactness
to a Scott-continuous relation β≪(−) (called way below)
on open subsets, and then requires that
| φ = ⋁↑ {βn ∣ βn≪φ}, or φ = ∃ n. βn∧ Anφ, where Anφ ≡ (βn≪φ), |
which is another basis decomposition, giving i and I as before.
These two definitions are actually different, in that
However, a space only carries a basis with both properties if it is itself compact and the intersection of any two compact subspaces is again compact; it is then called stably locally compact. See [G][JKM01] for the details of this approach to local compactness.
5.10.
We have shown that every locally compact Bourbaki space or locale is a
Σ-split subspace of ΣN.
So if we can prove that all such subobjects are locally compact locales
then we have a model of the monadic situation.
Locally compact locales and sober locally compact Bourbaki spaces
are equivalent, assuming the axiom of choice [Joh82, VII 4.5].
Recall from §4.4 that the Scott topology on ΣN is the free frame F N on the set N. For a Σ-split subspace X⊂ΣN, the topology L on X is a retract of F N, where H:F N↠ L and I:L↣ F N are Scott-continuous and satisfy H· I=id. Hence L is a continuous lattice [Joh82, VII 2.3].
The maps I and H need not be adjoint, but since H is a frame homomorphism, it has a right adjoint R that is monotone but not necessarily Scott continuous. Then id⊑ j≡ R· H=j· j preserves meets, making it a nucleus (§4.8), and H≡ i* and R≡ i*, where i:X⊂ΣN is the sublocale defined by j.
5.11.
Although we have now related Beck’s theorem in category theory
to ideas of general topology, these are still rather abstract.
We need a more compelling example from the applications of topology
to demonstrate that Σ-split subspaces are important to
the customers of this subject (cf. §3.5).
Recall from §§1.8 and 4.7 that the
classical Heine–Borel theorem fails in Russian Recursive Analysis but
holds in locale theory.
Now, it is possible to construct a “space of Dedekind cuts” in any category that has ℕ, powers of Σ, equalisers and some other properties Remark I 6.9. However, the “closed interval” [0,1] within this space need not be compact. The category of dcpos and Scott-continuous functions has the relevant structure, but the order on a dcpo determines its topology, and the “real line” is (uncountable but) discrete in both senses, so its only compact subspaces are finite sets.
5.12.
Beck’s theorem comes to the rescue.
The classical Heine–Borel theorem provides a Scott-continuous Σ-splitting I for the inclusion of the equaliser i:ℝ↣Σℚ×Σℚ, where i x≡(λ d.d< x,λ u.x< u). In traditional notation, this I is given by
| (V⊂ℝ) open ↦ {(D,U) ∣ ∃ d∈ D.∃ u∈ U.(d< u)∧[d,u]⊂ V}, |
or
| φ:Σℝ↦ λδυ.∃ d u. δ d∧υ u∧(d< u)∧∀ x:[d,u].φ x |
in the ASD λ-calculus.
The idempotent I·Σi can be shown to be equal to an expression that involves the rationals alone:
| (I·Σi)Φ (δ, υ) ≡ ∃ n≥ 1. ∃ q0 < ⋯ < qn. δ q0 ∧ υ qn ∧ ⋀k=0n−1 Φ(δqk, υqk+1). |
This satisfies the hypothesis of Beck’s theorem, so defines an object R of ASD. In R, the interval [0,1] is compact, and indeed this object satisfies all of the properties that one could reasonably require of a computable real number object [I]. Looking more closely at its topology, ΣR, it can be shown, as in the classical situation, that any open subspace is uniquely expressible as a countable disjoint union of open intervals, although the words “countable” and “interval” require some constructive qualification [J].
We now have enough experimental evidence to start writing down some axioms (§3.2), at least for locally compact spaces.


