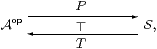



Now we begin to describe the ideas from traditional general topology that we shall take as the “client’s brief” for our new theory of that subject. We sketch the execution of this programme in the remainder of this paper. These ideas are presented in the form of universal properties, providing the leftmost arrow of the diagram in §3.1. Following the horizontal arrow there, we shall then develop a corresponding syntax. As far as possible, we do this in a general way that might be adapted to other subjects.
4.1.
The principal mathematical insight that we shall employ is
the duality between algebra and geometry.
Figures like circles and parabolae are defined by polynomials such as x2+y2−a2 and x2−2b y, and superposition of the figures corresponds to multiplication of their polynomials. Polynomials over a field that is algebraically closed may, like natural numbers, be expressed uniquely as products of irreducible or prime factors, which therefore capture the irreducible geometrical figures in a purely algebraic way.
By no means all commutative rings admit unique factorisation into primes, for example
| 3· 2 = 6 = (1+ | √ |
| )·(1− | √ |
| ) in ℤ[ | √ |
| ]. |
However, Ernst Kummer recovered the situation by introducing ideal numbers. The definition of an ideal that is now found in textbooks, as a subset of the ring with certain properties, is due to Richard Dedekind, who began the use of set theory to create mathematical objects.
Leopold Kronecker, on the other hand, preferred to treat equations themselves as names for their own roots. This is perhaps the point in the development of mathematics at which the classical and constructive traditions diverged.
The notions of ideal and prime may be transferred from rings to lattices by following the analogy between their operations. The systematic study of these ideas was undertaken by Marshall Stone [Sto37, Sto38]. Since geometry and algebra each have their own natural generalities, they need not coincide exactly: it may be necessary to make extensions, restrictions or other adjustments on both sides to achieve agreement.
4.2.
Putting Stone’s programme in categorical language, let A be some category
of “algebras” and S one of “spaces”, the exact nature of which
we leave open. Then by a Stone duality we mean an adjunction
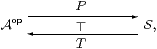
in which T X is the algebra (maybe of open subspaces) associated with a geometrical object X, and P A is the space of primes of an algebra A.
Because of the contravariance, the unit and counit of the adjunction (§2.4) go in the same direction in the categories S and A,
| ηX:X → P(T X) and ιA:A → T(P A). |
These say how each point defines a prime, and how the algebra is represented by its space of primes.
We call X a sober space if ηX is an isomorphism, i.e. every prime corresponds to a unique point, so a sober space is one that has exactly the points that are required by algebra. Similarly, A is a spatial algebra if it has enough primes to provide a faithful representation, making ιA invertible. The situation is a Stone equivalence if all spaces are sober and all algebras spatial, in which case the functors P and T are equivalences.
4.3.
Stone dualities often arise from a schizophrenic object Σ,
i.e. one that in some sense belongs to both categories, where
| T X ≡ S(X,Σ) and P A ≡ A(X,Σ). |
The abstract description of Stone duality that we have given comes, essentially, from the book [Joh82], which also provides an excellent and wide-ranging survey of concrete examples. In those that directly interest us, Σ is at least a distributive lattice, whose elements we sometimes regard as “truth values” (§7).
If you would like to apply the methods of this paper in another discipline, you will of course want to see what it can do for topology first. However, on your second reading you should stop here. You need to identify the object Σ in your subject. It is likely to be the most important algebraic or geometrical structure, albeit one that the undiscerning may have dismissed as trivial (§3.4). Do not be misled by our discussion of subobject classifiers in §7, or by the fact that all but two of the examples in [Joh82, §VI 4] are based on a two-element set — the other two use the line ℝ and the circle ℝ/ℤ. The natural numbers ℕ, integers ℤ, complex numbers ℂ, the closed interval [0,1]⊂ℝ and the ring K[x] of polynomials in one variable over a ground field play this key role in other mathematical settings.
The most important property of Σ that you should check is that all of the other desirable objects are sober with respect to it; this fact may already be a headline theorem in your subject. Then, ignoring the rest of §7, it may be worth looking for an algebraic property like that in §7.7; unlike sobriety, this may not have been recognised before.
4.4.
The textbook definition of topological spaces gives rise to a Stone duality
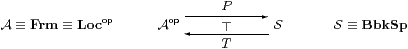
in which BbkSp is the category of Bourbaki spaces (what the textbooks call topological spaces, cf. §3.7) and continuous functions between them in the traditional sense.
The algebra T X associated with a Bourbaki space is simply its lattice of open subspaces. Discarding the points, what kind of algebra is it? It has finite meets and arbitrary joins, where binary meets distribute over arbitrary joins. A frame is exactly an algebra for these operations, and Frm is the category of frames and homomorphisms.
The functor Frm→Set that forgets this algebraic structure has a left adjoint, which provides the free frame F N on a set N. The elements of the free frame may be characterised in two ways, either as upper families U of finite subsets of N, i.e. if T⊃ S∈U then T∈U too [Joh82, II 1.2], or as Scott open families of arbitrary subsets of N.
How do we recover the points or primes of a frame A? They are continuous maps 1→ P A, which correspond under the adjunction to frame homomorphisms A→ T1. Since T1≅℘(1), these are subsets F⊂ A whose membership predicate is a frame homomorphism, so ⊤∈ F and if α,β∈ F then α∧β∈ F, whilst if ⋁αi∈ F then αi∈ F for some i.
4.5.
In our investigation of topology, we shall often find it helpful
to consider the analogy with discrete objects
(“sets” in the sense of §2.10).
Classically, there is a Stone equivalence CABAop≃Set,
where CABA is the category of complete atomic Boolean algebras
and homomorphisms for ⋁ and ⋀,
for which T X is the powerset of the set X
and P A is the set of atoms (minimal non-⊥ elements) of A.
This equivalence was proved by Adolf Lindenbaum and Alfred Tarski
[Tar35].
4.6. We want to design a new building to replace the old one functionally
and not extensionally (§3.7),
so it is really the underlying intuition
of Stone duality that we shall use.
The concrete examples can be a little distracting, especially with
regard to the notion of sobriety.
We defined this above in a way that depends on the choice of adjunction,
and so may vary from one application to another.
Classically, X is a sober space with respect to the concrete Stone duality between frames and Bourbaki spaces (§4.4) iff every irreducible closed subspace is the closure of a unique point. In particular, every Hausdorff space is sober in this sense [Joh82, II 1.6]. On the other hand, we shall see that the Hausdorff spaces ℕ and ℝ are sober with respect to our abstract Stone duality iff they admit definition by description (§9.11) and by Dedekind cuts (§11.11) respectively.
There is no theorem to say that the old and new definitions of sobriety are coextensive, simply because there is no common genus of which these are species. There is nothing to be gained by trying to find such a generality, as it would be artificial.
4.7.
One way to achieve Stone equivalence is just to replace
S by Aop.
In the cases where algebras are frames or commutative rings,
the new “algebraic” spaces are called locales
or affine varieties, respectively.
A continuous function f between the locales that correspond to
frames A and B is by definition a frame homomorphism f*:B→ A in the
opposite direction.
However, since any frame homomorphism preserves (finite meets and) all joins,
it has a right adjoint, and these are written f*⊣ f*.
Stone duality is now vacuous as an extensional theorem, instead serving as a vehicle for the intuitions of general topology and algebraic geometry, which may be used to reconstruct these disciplines in a new, algebraic, form [Joh82, Har77].
Locale theory mitigates a lot of the evils of point-set topology. For example, it is largely free of the axiom of choice, without which it is next to impossible to do anything with Bourbaki spaces. In particular, Peter Johnstone proved Tychonov’s theorem (that a product of compact spaces is compact) without it [Joh82, Thm. III 1.7]. Also, the closed interval [0,1] is Dedekind complete and compact (§1.8) in the localic reals over any elementary topos, whereas if we interpret the point-based definitions in the internal language of a sheaf topos, the object of Cauchy reals is typically smaller than the Dedekind one, and the Heine–Borel theorem fails [FH79].
4.8.
Whilst locale theory makes significant advances over traditional
topology
it still relies on the old foundations of the category of sets,
as of course do the other concrete examples in this section.
But our goal is to build new foundations for topology.
Nevertheless, locales provide a useful test-bed for many of the ideas that we shall consider. We shall in particular need to know about sublocales i:S↣ X, by which we mean coequalisers of frames. These have i*· i*=id, and are therefore captured by the other composite, j≡ i*· i*, which satisfies id⊑ j=j· j and preserves ∧, but usually not any kind of joins. An endofunction j of a frame with these properties is called a nucleus, and always arises from a sublocale in this way [Joh82, II 2.2]. In particular, an element a∈ A of a frame gives rise to the nuclei a⇒(−) and a∨(−), which encode the corresponding open and closed sublocales, respectively. We shall encounter localic nuclei in §§5.10, 6.6 and 7.5.


