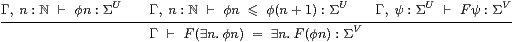



Although it is remarkable how much the theory already looks like traditional general topology without invoking it, we come to the point where we actually have to say that all functions are Scott continuous as an axiom.
Since this axiom completes the theory of locally compact spaces, we are moving into the territory of a user-oriented account (cf. §3.8), but certain foundational issues remain. One of these is the question of which statement of the Scott continuity axiom we should adopt, since there are several candidates that arise from some of the applications of this idea.
11.1.
Denotational semantics generalises the notion of recursion from
minimalisation (µ, §9.12) to fixed points of operators
of higher types.
Applying the operator F repeatedly to ⊥
gives an increasing sequence φ n≡ Fn⊥.
Then F fixes the join of such a sequence if we assume the rule
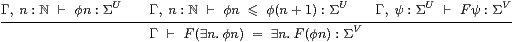
|
In this case, every space has and every map preserves joins of definable ascending chains with respect to the ⊑ order (§8.2). Also, on any object that has ⊥, every endomorphism has a least fixed point [Tay91].
11.2.
Turning to real analysis,
a common use of the Heine–Borel theorem (§1.8)
is to derive a uniform value that is valid throughout
a compact space K from local values at each point.
For example, b:ℝ is an upper bound on a function f:K→ℝ
at x if θ(x,b)≡(f x< b)⇔⊤.
Then θ is monotone in the sense of taking
the imposed arithmetical order ≤ on ℝ
to the intrinsic one ⇒ on Σ:
| …, b≤ b′ ⊢ θ(x,b) =⇒ θ(x,b′). |
The δ> 0 that is used in the ε–δ definitions of continuity, differentiability, etc. , is similar, but the defining property reverses the arithmetical order:
| …, 0<δ≤ δ′ ⊢ θ(x,δ) ⇐= θ(x,δ′). |
In either case, by compactness, the quantifier ∀K satisfies
| ∀ k.∃ b.θ(k,b) =⇒ ∃ b.∀ k.θ(k, b). |
In Section J 9–10 this is used to prove that any expression Γ,x:ℝ⊢ a:ℝ is continuous in the ε–δ-sense, and uniformly so on any compact domain.
This principle, in which the second argument of θ ranges over ℝ, is equivalent to its analogue with ℚ instead. The latter is preferable foundationally (cf. §3.8), as we would like to work with overt discrete spaces (§9).
11.3.
The indexing objects ℕ and ℚ in these two properties
have max operations, whilst we may form binary unions of
finite open subcovers, so the common pattern is a directed join.
In practice, we have a set (overt discrete space) N of indices,
equipped with an imposed semilattice operation (+).
Then we select an open subsemilattice of N classified by α:ΣN.
As in §5.8, we use sub- and super-scripts to indicate
co- and contra-variance with respect to this imposed order on N.
Then a directed join, written
| ⋁{n:N ∣ αn}↑ φn ≡ ∃ n:N.αn∧φn, |
involves a pair of families (αn,φn) such that
| ⊤⇔∃ n.αn, αn∧αm⇔αn+m and φn∨φm⊑φn+m. |
Then we say that F preserves this join if F(∃ n.αn∧φn) = ∃ n.αn∧ Fφn.
To do this, + does not actually need to satisfy the equations for a semilattice, so the leading examples of (N,+) are (ℕ,max), (ℚ,max), (ℚ,min), (K(M),∪) and (List (M),+) for any overt discrete M.
11.4.
In the first instance we shall be content with N≡ℕ,
although it is equivalent but more useful to take N≡T instead,
since List (T)≅T (§9.6).
For either of these Ns,
we assert the Scott continuity axiom in the form
| F:ΣΣN, φ:ΣN ⊢ Fφ ⇔ ∃ℓ:List N.F(λ n.n∈ℓ) ∧ ∀ n∈ℓ. φ n. |
Consider in particular φ≡λ x.σ and F≡λψ.G(ψ 0), for any given σ:Σ and G:ΣΣ. Since it’s decidable whether a list is empty or inhabited, ∃ℓ reduces to the disjunction of these two cases, so
| Gσ ≡ Fφ ⇔ G⊥ ∨ σ∧ G⊤. |
Hence the Phoa principle follows from that of Scott.
11.5.
The Scott axiom for N says that ΣN has a basis
as a locally compact space, in the sense of §§5.8f, with
| βℓ ≡ λ n.n∈ℓ and Aℓ ≡ λφ.∀ n∈ℓ.φ n. |
This corresponds to the classical description of the Scott topology on ℘(N), whose open sets are U≡{U⊂ℕ ∣ ℓ⊂ U} for all finite ℓ⊂ℕ.
Another way of putting this is that ΣΣN is a retract of ΣN, and it is not difficult to extend this to all objects that are definable using × and Σ(−). Hence any object that is definable in the monadic framework (§6) is a Σ-split subspace of ΣN [Section C 8].
[G] goes on to show how any computably based locally compact Bourbaki space or locale X may be “imported” into ASD. That is, suppose that X has a basis (Kn,Vn) indexed by N, such that the relation (n≺≺ m)≡(Kn⊂ Vm) is recursively enumerable. Then this relation is a term n,m:N⊢(n≺≺ m):Σ satisfying certain properties [Section G 11], from which we may define a nucleus on ΣN [Section G 14], and so a type whose interpretation is X [Section G 17].
11.6.
It is in this representation that we can show that
the λ-calculus definitions of primes and nuclei
(§§6.3 & 6.6)
are equivalent to more familiar lattice-theoretic ones
[Section G 10].
We can also characterise certain classes of definable objects [Section G 9]:
From (a) we may derive definition by description (§9.11), the free monoid (List (N), §9.7) and the Scott principle (§11.4) for all overt discrete N.
Beware, however, that all of these results apply just to objects that are definable in the monadic framework as we gave it in §6. They will need to be proved again, or may cease to be valid, in a more general setting (§12).
11.7.
Even without assuming that N is definable, we may use the intuitions
gained from these results to construct List (N) for any overt discrete N.
The key idea is to encode any Kuratowski-finite ℓ⊂ N
by the pair of modal operators (§8.8)
that say that ℓ is overt and compact.
Then List (N) is a Σ-split subspace of
ΣΣN×ΣΣN.
It is obtained using a nucleus that is itself defined as a fixed point,
using the basic Scott continuity axiom (§11.1)
and a tour de force of techniques in ASD and domain theory
[E].
We deduce that the overt discrete objects form an arithmetic universe (§9.7).
11.8.
The general Scott continuity axiom in §11.4 is only meaningful
for general overt discrete N that have List (N) or K(N).
But we may obtain the latter from either
Armed with these, we are in a position to assert the Scott continuity axiom (§11.4) for general overt discrete N.
In the setting of classical topology, the weaker axiom would only provide countable unions of open sets, whereas arbitrary cardinalities are required for the usual theory.
Similarly, in the context of our underlying set axiom, Scott continuity for general general overt discrete objects is exactly what is required to make the monad in §10.5 agree with the one that defines the category of frames over E (§4.4). The full subcategory of spaces with enough points and enough opens then agrees with the category of sober Bourbaki spaces over E.
11.9. Turning to the applications of general topology in elementary real analysis,
this axiomatic setting (in fact, with just §11.1)
is enough to construct the Dedekind reals using the nucleus
that we mentioned in §5.12 [I].
We may use this as an experimental test of the prototype axioms (cf. §3.2). The claim is that ASD is a theory of computable topology, and in particular that its terms x:ℝ⊢ a:ℝ exactly capture the computably continuous functions f:ℝ→ℝ. We already know that the interpretation of such a term in the model using locally compact locales (§5.10) is continuous, whilst [K] gives some ideas of how to compute with our calculus.
So, is every classically continuous function f:ℝ→ℝ that can be computed by a program representable in ASD? First we need to agree on some notion of computability, but whatever yours is, I would hope that it could be adapted to provide a program π(q,e,t) that takes three rational arguments and terminates iff e< f(q)< t. Using the denotational semantics of your programming language, interpreted in the domain theory of ASD, π is a term of type Σℚ3. From this we may derive a morphism g:ℝ→ℝ in ASD whose classical interpretation is the given function f.
11.10.
In foundational studies it has been long been customary to regard
ℝ as something constructed from ℕ (cf. §2),
and indeed that is what we too have done [I].
However, the importance of ℝ throughout mathematics and
science surely justifies introducing it as a base type,
especially if we can formulate convincing axioms for it.
For these, we propose that
| y> 0 ⇒ ∃ n:ℤ. y(n−1) < x< y(n+1). |
11.11.
Dedekind completeness plays the same role for ℝ that
definition by description (§9.11) does for ℕ,
namely to recover numbers from the computation that we do in the
arena of logic.
Cuts and primes are inter-definable by
| (δ,υ) ≡ (λ d.P(λ x.d< x), λ u.P(λ x.x< u)) |
and
| P ≡ λφ.∃ d< u.δ d∧υ u∧∀ x:[d,u].φ x, |
showing that Dedekind completeness cannot really be separated from the Heine–Borel theorem (Section I 14).
Once again, there is a system of logical rules, in which the definition of a Dedekind cut is the premise of the introduction rule for cut (δ,υ), and the elimination rule represents any a:ℝ by the cut
| δ ≡ λ d.d< a υ ≡ λ u.a< u. |
Like focus and descriptions, Dedekind cut operations may be eliminated everywhere except on the outside of a term. Any cut sub-term has a smallest enclosing sub-term [cut /x]*σ of type Σ (typically <, ≠ or >), and then
| [cut (δ,υ)/x]*σ ⇔ (λ x.σ)cut (δ,υ) ⇔ ∃ d< u:ℚ.δ d∧υ u∧∀ x:[d,u].σ. |
11.12. The applications of this construction to elementary real analysis
are begun in [J].
The principal objective of this paper is to solve equations
defined by continuous functions f:ℝ→ℝ,
which makes novel use of overt subspaces.
By way of an experimental test of our axioms for ℝ
(cf. §3.2),
it also proves the traditional characterisation of open subspaces of ℝ
as countable unions of disjoint open intervals,
although the words “countable” and “interval” need some qualification.
This result fails in real analysis without the Heine–Borel theorem,
in particular in Bishop’s theory [BB85].
From here there should be no difficulty in developing a theory of differential and integral calculus on ℝn. However, since the version of ASD that we have developed so far only gives an account of locally compact spaces, we cannot study Banach spaces and functional analysis until we have a much more general framework than the one in §6.


